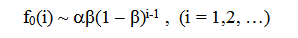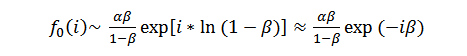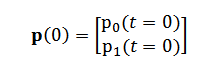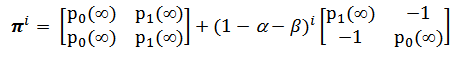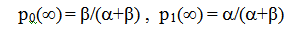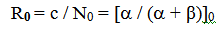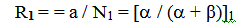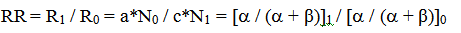Аппарат теории цепей Маркова в профэпидемиологии

Г.В.Федорович ООО «НТМ-Защита», Москва

Введение.

В наших предыдущих статьях [1 – 3] было показано, что анализ заболеваемости с временной утратой трудоспособности (далее - ЗВУТ) дает адекватную характеристику условий на рабочих местах. В частности, по уровню ЗВУТ можно оценить классы условий труда в различных подразделениях предприятия [2], а по нозологической структуре ЗВУТ, именно - по данным о количестве лиц с ЗВУТ различных нозологических форм - можно оценить этиологию, т.е. виды и уровни наиболее существенных ВПФ, действующих на работников [3].

Следует отметить, что согласно основному документу [4], определяющему методику углубленного изучения ЗВУТ, рекомендуемый объем информации о ЗВУТ включает как данные о количестве К случаев ЗВУТ, так и сведения о суммарной длительности D ЗВУТ в обследуемом рабочем коллективе. Один из распространенных способов интерпретации результатов эпидемиологических исследований профессионально обусловленных заболеваний (далее - ПОЗ) проанализирован в работе [5]. Рассматривалась возможность использования 2х2 таблиц сопряженности для надежной и непротиворечивой оценки степени (условной вероятности) влияния вредных производственных факторов (далее – ВПФ) на уровень хронических ПОЗ. Проблемы возникают при попытке использовать такие таблицы для анализа ЗВУТ. В частности, неясно – какие именно величины (количество случаев К, суммарную продолжительность D, или их комбинацию) следует использовать для характеристики ЗВУТ. Кроме того, обе величины относятся к заболевшим работникам. В таблицу сопряженности следует вносить также данные о работниках, оставшихся здоровыми, несмотря на воздействие ВПФ, при этом неясно – какими величинами пользоваться здесь.

В указанных работах использовались характеристики ЗВУТ, вводимые, в значительной степени, произвольно. Целесообразно обосновать те или иные решения для надежной оценки рисков (оценочных, относительных, атрибутивных) – главного, для чего предназначены таблицы сопряженности. Это сделано ниже.

1.Цепи Маркова как основа анализа результатов исследований ЗВУТ

1.1. Наиболее характерны в эпидемиологии профессиональных заболеваний когортные исследования. Они могут быть как ретроспективными, так и перспективными, их результаты могут быть охарактеризованы как «продольные», т.е. они либо относятся к периоду наблюдений (например, число К случаев ЗВУТ), либо сами описывают продолжительность наблюдаемых явлений (например, суммарная длительность D ЗВУТ). Их можно использовать для расчета «поперечных» характеристик ЗВУТ, например – среднего числа n болеющих в обследуемом коллективе. Как показано в [6], величина n связана с D формулой n = D/Y. Кроме того, по К и D можно определить среднюю длительность заболевания l = D/K , а также среднюю длительность периодов между заболеваниями L = N*Y/K . Легко видеть, что n/N = l/L .

Величины, обратные средним длительностям α = 1/L и β = 1/l допускают наглядную интерпретацию как вероятность заболеть (будучи здоровым) и вероятность выздороветь (будучи больным). Обе вероятности относятся к промежутку времени Δt = 1 сутки. Величины 1 - α и 1 – β определяют вероятности остаться здоровым или больным соответственно. Заметим, что вероятность α определяется, в значительной степени, условиями на производстве, в то время как вероятность β, в большей степени, отражает условия реабилитации – бытовые, медицинского обслуживания и т.п.

Очевидно, справедливо следующее утверждение: если работник сегодня с вероятностью р0 здоров или с вероятностью р1 болен (разумеется, р0 + р1 = 1), то завтра он будет здоров с вероятностью (1 - α)р₀ + βр₁ , а с вероятностью αр₀ + (1 - β)р₁ заболеет. Несложно рассчитать вероятности быть больным или здоровым на послезавтра и на последующие дни. Описанная последовательность представляет собой простейший вариант процесса, известного в статистике как цепь Маркова (см. напр. [7]). Развит эффективный аппарат математического анализа таких последовательностей. Им можно воспользоваться для анализа данных о ЗВУТ на различных производствах.

1.2. Анализ цепи Маркова позволяет оценить распределение больных по срокам их болезни. Рассмотрим отдельного работника. Состояние «здоров» будем отмечать как состояние 0, соответственно «болен» - как 1. Отсчет времени начнем с момента его заболевания, т.е. считаем, что в момент t = 0 произошел переход из состояния 0 в состояние 1. Вероятность этого события α . Рассмотрим случайную величину T, обозначающую время первого возвращения в состояние 0. По определению, T = i Δt , если в моменты времени t₁, t₂, … t_i-1 система остается в состоянии 1. Каждое такое событие происходит с вероятностью 1 - β , так что вероятность остаться больным в течение времени T = i Δt равна (1 – β)^i-1. В момент времени ti происходит возвращение в состояние 0. Вероятность последнего события β . Результирующий закон распределения f0(i) случайной величины T имеет вид:

Коэффициент пропорциональности определяется условием нормировки функции f0(i). Можно записать это выражение в несколько ином виде:

В последнем соотношении использовался факт реальной малости величины β , что позволяет записать ln(1 - β) ≈ - β . Условие нормировки f₀(i) на единицу приводит к окончательному выражению

Соотношение (3) можно ассоциировать с распределением длительностей ЗВУТ, полученным ранее в работе [6], при анализе ансамблевых средних в трудовых коллективах. Как отмечалось в этой работе, статистика ансамблей дает адекватную форму описания систем, состоящих из множества подобных элементов. То обстоятельство, что анализ ситуации с ЗВУТ в трудовых коллективах с использованием методов теории цепей Маркова дает ту же форму представления результатов, что и статистика ансамблей, свидетельствует об адекватности такого подхода.

1.3. Рассмотрим эволюцию начального распределения больных и здоровых. Представим его в виде вектора-столбца:

Вероятности переходов π00 = 1 - α , π01 = β , π10 = α и π11 = 1 - β образуют матрицу переходов π = πjk (j,k = 0,1) . Очевидно, что случай α + β = 0 (т.е. α = 0 и β = 0) не представляет интереса, т.к. в такой системе ничего не меняется: больные остаются больными, здоровые – здоровыми. Аналогично, неинтересен и случай α + β = 2 (т.е. α = 1 и β = 1), т.к. в такой системе на каждом шаге состояние неслучайно меняется на прямо противоположное. В дальнейшем будем полагать, что |1 - α - β| < 1 .
Вектор вероятностей p в момент времени ti = i Δt определяется матричным уравнением

Для дальнейшего представляют интерес несколько результатов теории цепей Маркова:
(1)Последовательное применение операции (5) к начальному состоянию р(t=0) приводит к распределению вероятностей состояния на i-том шаге:

(2)Для i-той степени матрицы перехода π можно записать выражение:

где обозначено

Так как |1 -α - β| < 1 , то с ростом числа шагов i в выражении (7) для матрицы πi остается только первое слагаемое.
(3)Подставляя выражение (7) в формулу (6), получим:

Как и в (7), последнее слагаемое в сумме (9), содержащее параметры начального распределения вероятности, убывает с ростом i , так что соотношения (8) действительно определяют распределение вероятности обнаружить здорового или больного работника после достаточно большого интервала от начала отсчета времени. Оно не зависит от начального распределения. В теории цепей Маркова распределение вероятности p(∞) называется финальным. Так же, как и начальное, финальное распределение удовлетворяет условию нормировки р0 + р1 = 1 . Непосредственной подстановкой нетрудно убедиться, что финальное распределение удовлетворяет уравнению

то есть, приблизившись к финальному распределению, вероятности не будут меняться от звена к звену в цепи Маркова. В этом смысле финальное распределение является равновесным – сколько человек заболевает в единицу времени, столько же и выздоравливает.

1.4. Определение (8) финального распределения больных и здоровых через вероятности заболеть α и выздороветь β является нетривиальным результатом теории цепей Маркова. Непосредственная проверка справедливости этого результата на конкретном материале эпидемиологических исследований затруднительна. Веским аргументом в его пользу является отмеченное выше совпадение формы выводов теории цепей Маркова и статистики ансамблей ЗВУТ в трудовых коллективах. В этой связи следует отметить, что в работе [6] прослежены параллели между эпидемиологическим описанием профессионально обусловленных заболеваний и их описанием на языке статистики ансамблей. Это обстоятельство позволяет надеяться, что и результаты теории цепей Маркова можно интерпретировать в системе эпидемиологических понятий.

2.Способы интерпретации результатов.

2.1. Один из распространенных способов интерпретации результатов эпидемиологических исследований профессионально обусловленных заболеваний (ПОЗ) проанализирован в работе [5]. Рассматривалась возможность использования 2х2 таблиц сопряженности для надежной и непротиворечивой оценки степени (условной вероятности) влияния ВПФ на уровень хронических ПЗ. Проблемы возникают при попытке использовать такие таблицы для анализа ЗВУТ. Во-первых, для характеристики уровня ЗВУТ принято использовать два параметра – количество случаев К и суммарную продолжительность D. Неясно, какие именно величины следует подставлять в колонку таблицы ПОЗ=1 (а и с в обозначениях [5]). Во-вторых, обе величины относятся к заболевшим работникам. Неясно, какими величинами b и d следует характеризовать здоровых работников. Последнее необходимо для оценок рисков (оценочных, относительных, атрибутивных) – главного, к чему приводит использование таблиц сопряженности.
Ответы на оба вопроса дают оценки (8) финальных вероятностей обнаружить работника здоровым или больным. Если обозначить через N1 численность работников, подвергающихся воздействию ВПФ, а через N0 , соответственно, численность контрольной группы, то следует полагать a = N1[α/(α+β)]1 , b = N1[β/(α+β)]1 . Здесь индексом 1 отмечены величины, относящиеся к работникам, подвергающимся воздействию ВПФ. Для контрольной группы c = N0[α/(α+β)]0 , d = N0[β/(α+β)]0 . После этого все величины, характеризующие риски ЗВУТ, оцениваются по тем же правилам, что и риски хронических ПЗ.

Определяются следующие виды риска:

• Оценочный риск заболевания – отношение числа случаев заболевания в когорте к численности когорты: (a + c)/(N0 + N1)

• Риск возникновения заболевания в группе, не подверженной воздействию ВПФ:

• Риск возникновения заболевания в группе, подверженной воздействию ВПФ:

• Относительный риск (RR) – величина, описывающая увеличение риска заболевания под действием ВПФ. Это отношение вероятности заболевания у работников подвергающихся воздействию ВПФ к вероятности заболевания у работников, не подвергающихся такому воздействию.

2.2.Продемонстрируем возможности использования таблиц сопряженности для анализа воздействия вредных производственных факторы на работников, занятых в сварочном производстве, на трех крупных предприятиях машиностроения в г. Санкт - Петербурге: ОАО «Ижорские заводы», ФГУП «Адмиралтейские верфи» и ОАО судостроительный завод «Северная верфь» [8]. Для анализа использовались данные за 2007, 2008, 2009 гг.

Из основной группы (электросварщики) и контрольной группы (токари, фрезеровщики, слесари) было подобрано 170 пар (т.е. N0 = N1 =170), метчированных по возрасту и стажу между основной и контрольной группами. Исходные данные по основным показателям ЗВУТ исследуемых групп приведены в табл.1

Таблица 1

Характеристики ЗВУТ по основной и контрольной группам

Заметим, что средние длительности l заболеваний в основной и контрольной группах расходятся незначительно (менее 4 %). Можно сделать вывод, что условия реабилитации (бытовые, медицинского обслуживания) в этих группах близки. В то же время периоды между заболеваниями заметно различаются (более 16 %), что свидетельствует о заметных различиях в условиях труда.

Построенная методом анализа цепей Маркова таблица сопряженности имеет вид:

Таблица 2

Таблица сопряженности состояния респираторного здоровья работников

Анализ данных табл.2 с использованием соотношений разд.2 позволяет утверждать следующее:

• Оценочный риск ЗВУТ в обследованном коллективе составляет 0,035.
• Риск ЗВУТ в группе, подвергающейся воздействию ВПФ, составляет 0,039.
• Риск ЗВУТ в группе, не подвергающейся воздействию ВПФ, составляет 0,032.
• Относительный риск RR = 1,20 ; соответственно, этиологическая доля EF = 16,5 % Согласно Руководству [10] такие величины RR и EF свидетельствуют о малой степени причинно-следственной связи нарушений здоровья с работой.

Заключение.

Предложен вариант реализации модели, основанной на применении теории простой цепи Маркова для анализа профессионально обусловленной ЗВУТ. Определены параметры, являющиеся входными в модель и позволяющие получить характеристики продолжительности периодов здоровья и болезни. Подход позволяет наиболее оптимально использовать эпидемиологическую информацию для уменьшения рисков в хозяйственной деятельности конкретного предприятия.

Эпидемиологический анализ таблиц сопряженности так же важен, как и изучение распределения вероятностей в статистике ансамблей трудовых коллективов. Эти результаты дополняют друг друга при решении различных прикладных задач.

Статистические характеристики, полученные методом анализа цепей Маркова, при их адекватности фактическому материалу, определяют профессиональные риски, связанные с производственной деятельностью. Прогноз заболеваемости, составленный на основании цепей Маркова, можно отнести к разряду инерционных прогнозов в вероятностной форме, который, при условии адекватности модели фактическим данным, может значительно повышать качество обеспечения эпидемиологической информацией различных областей производственной деятельности.

Литература

1. Федорович Г.В. Классификация условий труда по эпидемиологическим даннм // БиОТ. – 2011. - № 4. – С. 49 –52.
2. Федорович Г.В. Профессиональный риск: количественная оценка и управление // БиОТ. – 2012. - № 1 – С. 60 – 64.
3. Федорович Г.В. Этиологические структуры профзаболеваний // БиОТ. – 2012. - № 4 – (в печати).
4. Методические рекомендации по углубленному изучению заболеваемости с временной утратой трудоспособности. Минздрав СССР, № 2484-81, 1981.
5. Федорович Г.В. Эпидемиологический анализ характеристик профессионального риска // БиОТ – 2012 - № 3 – С. 41 – 45.
6. Федорович Г.В. Статистика ансамблей в расчетах профессиональных рисков // БиОТ – 2010 - № 4 – С. 48 – 52.
7. Тихонов В.И., Миронов В.А. Марковские процессы. - М.: Советское радио, 1977 - 488 с.
8. Кусраева З.С. Современный подход к оценке профессионального риска при выполнении электродуговой сварки и резки металлов // Доклад на XI съезде гигиенистов. М., апрель 2012 г.
9. Р 2.2.1766-03 «Руководство по оценке профессионального риска для здоровья работников. Организационно-методические основы, принципы и критерии оценки». - М.: Минздрав России, 2004. – 17 с.