Эпидемиологический анализ характеристик профессионального риска.

Г.В.Федорович,
ООО «НТМ-Защита», г. Москва

1.Введение.

В работе [1] была поставлена проблема адекватного структурирования данных для статистического анализа профессионального риска. Это необходимо для эффективной работы создающейся информационной системы АС «Профессиональные риски», объединяющей на общероссийском уровне базы данных о состоянии условий труда и показатели заболеваемости работников. Переход к комплексному описанию профессиональных рисков (ПР) открывает возможность выявления связи между объектами исследования - вредными производственными факторами (ВПФ) и профессионально обусловленной заболеваемостью (ПОЗ) работников. В самом общем случае, представляющие практический интерес ответы могут быть получены при статистическом корреляционном анализе данных. Корреляционный анализ позволяет определить наличие связи между величинами, характеризующими предполагаемые причину и следствие. Вычисляя коэффициент корреляции, можно оценить, насколько тесна и существенна связь «ВПФ - ПОЗ». Полную картину корреляционной связи дает представление ситуации в трудовом коллективе на фазовой плоскости с координатами: интенсивность ВПФ (вдоль оси абсцисс) и уровень ПОЗ (вдоль оси ординат). N точек (по числу работников) образует «облако», форма которого дает наглядную картину (характер и степень связи) статистической зависимости ПОЗ от ВПФ (см. подробнее [1]). Для количественной характеристики степени связи можно использовать коэффициент линейной корреляции (коэффициент Пирсона). Если связь статистически значима, можно оценить количественную зависимость заболеваемости y от интенсивности x воздействия ВПФ : y = α+β*x . Коэффициенты α и β определяются методом регрессионного анализа данных. Все это рутинные процедуры статистического анализа (см.напр. [2]).

В эпидемиологии (в том числе и эпидемиологии ПОЗ) приняты упрощенные методы описания и анализа ситуации с заболеваемостью в обследуемых группах. Предположим, что интенсивность x воздействия ВПФ имеет r градаций (или уровней) Х₁, Х₂ … Х_r, а уровень заболеваемости y имеет s градаций Y₁, Y₂, … Y_s. Вертикальные линии, проведенные через точки X_i (i = 1, … ,r) и горизонтальные, проведенные через точки Y_j (j = 1, … ,s) разбивают фазовую плоскость на ячейки (см. Рис.1). Если количества nij точек, попавших в соответствующие ячейки, занести в таблицу, состоящую из r строк и s столбцов, то получим таблицу сопряженности, обычно использующуюся в эпидемиологии ПОЗ. Метод построения приводит к очевидному свойству таких таблиц: если между x и y имеется статистически значимая связь, максимальные величины n_ij группируются вдоль диагонали таблицы сопряженности. Статистический характер результатов приводит к тому, что некоторое число точек попадает в недиагональные ячейки таблицы. При этом перед исследователем встает задача определить - насколько уверенно можно предсказать одну величину по значению другой.

Рис.1 Разбиение фазовой плоскости на ячейки.

В отличие от регрессионного анализа, в данном случае представляет интерес не столько конкретные значения коэффициентов в зависимости y от x, сколько надежная и непротиворечивая оценка степени и характера влияния ВПФ на уровень ПОЗ. Переводя проблему в практическую плоскость, следует оценить условную вероятность уровня ПОЗ при наблюдаемом значении ВПФ. Эта проблема рассматривается ниже.

Специфической для эпидемиологии ПОЗ является проблема множественности откликов организма работников на воздействие ВПФ. Действительно, один и тот же фактор может вызывать заболевания различных нозологических форм (НФ). Например, неблагоприятное воздействие микроклимата производственных помещений может приводить к заболеваниям органов дыхания, костно-мышечной системы, органов пищеварения и т.п. (см.напр. [3]). В этом случае таблица сопряженности становится многомерной. Для ее анализа можно использовать те же методы (см.напр. [4]), что и для одномерных таблиц, однако, результаты не столь наглядны и не допускают непосредственной интерпретации в эпидемиологических терминах. Возможные обобщения методов анализа одномерных таблиц на случаи ПОЗ множественных НФ также рассмотрены ниже.

2.Таблицы сопряженности признаков.

2.1. Вероятностные характеристики. В традиционной отечественной системе гигиенических характеристик условий труда обычно констатируется только факт (без количественной оценки) превышения нормативов ВПФ. Для таких исходных данных при переходе от фазовой плоскости к таблице сопряженности следует использовать дихотомическую (по шкале «да-нет») градацию как интенсивности воздействия ВПФ, так и уровня заболеваемости. Суммирование точек при этом проводится по частям фазовой плоскости «ВПФ-ПОЗ», разграниченными линиями x = X₀ и y = Y₀ (жирные линии на Рис.1). Предполагаем, что ВПФ действует (ВПФ = 1) только в области x > X₀ и не действует (ВПФ = 0) в остальной части фазовой плоскости (x < X₀ ). Аналогично, группы работников с низкой заболеваемостью y < Y₀ считаются здоровыми (ПОЗ = 0), а к группам болеющих (ПОЗ = 1) относят только те, заболеваемость в которых превышает уровень Y₀ .

Так отформатированные результаты принято размещать в 2х2 таблице сопряженности:

Таблица 1

Таблица сопряженности
результатов эпидемиологических исследований профзаболеваний

Несмотря на свою простоту, такой метод представления результатов обеспечивает возможность проведения глубокого нетривиального анализа.

Остановимся на смысле отдельных чисел в таблице. Величина а - это число заболевших (ПОЗ = 1) работников, подвергавшихся действию ВПФ, b - число работников, подвергавшихся действию ВПФ, но не заболевших (ПОЗ = 0). Соответственно, a + b - это суммарное число работников, подвергшихся действию ВПФ. Величина с - это число заболевших (ПОЗ = 1) работников, не подвергавшихся действию ВПФ, d - число работников, не подвергавшихся действию ВПФ и не заболевших (ПОЗ = 0). Соответственно, с + d - это суммарное число работников, не подвергшихся действию ВПФ. При суммировании по столбцам получим полное число а + с заболевших работников и число b + d работников, оставшихся здоровыми в течение срока исследования.

Данные табл.1 позволяют перейти от случаев к вероятностям. Например, вероятность заболеть Р(ПОЗ = 1) в обследованном коллективе определяется соотношением

Р(ПОЗ = 1) = (a + c) / N (1)

Вероятность попасть под действие ВПФ Р(ВПФ = 1) равна

Р(ВПФ = 1) = (a + b) / N (2)

Можно оценить условную вероятность для работника заболеть, если на него действует ВПФ:

Р(ПОЗ = 1 | ВПФ = 1) = a / (a + b) (3)

Последнюю вероятность следует отличать от вероятности обнаружить воздействие на работника ВПФ, если известно, что он заболел:

Р(ВПФ = 1 | ПОЗ = 1) = a / (a + c) (4)

Вероятности (1-2) можно рассматривать как априорные, а (3-4) - как апостериорные. Как таковые, они подчиняются соотношению, известному как теорема Байеса:

Р(ПОЗ = 1 | ВПФ = 1) = Р(ВПФ = 1 | ПОЗ = 1)*Р(ПОЗ = 1) / Р(ВПФ = 1) (5)

Аналогичные соотношения можно выписать и для вероятностей, соответствующих отсутствию ВПФ или заболевания.

Связь данных таблиц сопряженности с априорными и апостериорными вероятностями приводит к возможности использования аппарата вероятностной Байесовской логики. Это направление оказалось весьма плодотворным при анализе экологических и медицинских данных. В последнее время методы Байесовской классификации и Байесовского вывода использовались также и в области оценки условий труда [5] [6].

В случае существования однозначной зависимости «ВПФ-ПОЗ» в таблице сопряженности недиагональные элементы с и d должны были бы быть равны нулю. Реально, однако, существует «фоновая» вероятность заболевания (без влияния ВПФ). Она определяется соотношением

Р(ПОЗ = 1 | ВПФ = 0) = c / (c + d) (6)

Вообще говоря, существует также ненулевая вероятность остаться здоровым при действии ВПФ:

Р(ПОЗ = 0 | ВПФ = 1) = b / (a + b) (7)

Отличие от нуля вероятностей (6) и (7) исключает однозначность зависимости «ВПФ-ПОЗ», однако, в этом случае можно поставить вопрос о статистической связи признаков ВПФ и ПОЗ. Они могут считаться независимыми, если для совместной вероятности Р(ВПФ;ПОЗ) имеет место соотношение

Р(ВПФ;ПОЗ) = Р(ВПФ)*Р(ПОЗ) (8)

Если данные (количества работников) в клетках таблицы сопряженности были бы независимы, то их можно было бы определить по формулам:

а₀ = (a+b)*(a+c)/N ; b₀ = (a+b)*(b+d)/N ; c₀ = (a+b)*(c+d)/N ; d₀ = (c+d)*(b+d)/N (9)

Степень зависимости данных можно определить, вычисляя разности а-а₀ , b-b₀ … . Общепринятым критерием независимости данных в таблицах сопряженности является критерий χ² (К.Пирсон, Р.Фишер), определяемый как сумма квадратов разностей, деленных на ожидаемые количества работников а₀ , b₀ … :

χ² = N*(ad-bc)²/(a+b)/(a+c)/(b+d)/(c+d) (10)

Величинаχ² растет с ростом объема выборки N. От этого недостатка свободен критерий φ, определяемый по формуле

χ = φ/N^1/2 (11)

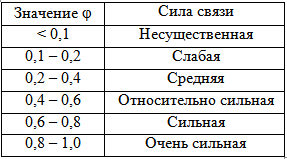
Величина φ может меняться от 0 (отсутствие связи) до 1 (однозначная зависимость). Более детальная статистическая интерпретация величины критерия φ приведена в табл. 2:

Таблица 2

Интерпретация значений критерия φ

Если зависимость «ВПФ-ПОЗ» значима, можно оценить добавочную вероятность заболевания δP, обусловленную воздействием ВПФ. Она определяется разностью между вероятностью заболевания при действии ВПФ: Р(ПОЗ=1|ВПФ=1) (см. ф-лу (3)) и «фоновой» вероятностью: Р(ПОЗ=1|ВПФ=0) (см. ф-лу (6)) :

δP = Р(ПОЗ=1|ВПФ=1) - Р(ПОЗ=1|ВПФ=0) = (a*d - b*c)/(a+b)/(c+d) (12)

2.2. Эпидемиологические характеристики. Таблицы сопряженности применяются для анализа эпидемиологических данных. В этой области, однако, используется специфическая терминология, обусловленная, в том числе, типом проводимого эпидемиологического исследования.

При проведении когортного исследования выявляется воздействие ВПФ на заболеваемость, т.е. устанавливается фактор риска. Соответственно, определяются следующие виды риска:

• Оценочный риск заболевания - отношение числа случаев заболевания в когорте к численности когорты. В терминах вероятностей эта величина равна Р(ПОЗ=1) (см. ф-лу (1)).
• Риск возникновения заболевания в группе, подверженной воздействию ВПФ. Это условная вероятность R₁ = Р(ПОЗ = 1|ВПФ = 1) (см. ф-лу (3)).
• Риск возникновения заболевания в группе, не подверженной воздействию ВПФ. Это условная вероятность R₀ = Р(ПОЗ = 1|ВПФ = 0) (см. ф-лу (6)).
• Относительный риск (RR) - величина, описывающая увеличение риска заболевания под действием ВПФ. Это отношение вероятности заболевания у работников подвергающихся воздействию ВПФ к вероятности заболевания у работников, не подвергающихся такому воздействию.

RR = R₁ / R₀ = a*(c+d)/c/(a+b) (13)

С относительным риском непосредственно связана этиологическая доля

EF = (RR-1)/RR = (a*d - c*b)/a/(c+d) (14)

• Атрибутивный (абсолютный) риск AR - дополнительный риск заболевания, обусловленный ВПФ. Эта величина эквивалентна добавочной вероятности δP (см. ф-лу (12)).

При исследованиях случай-контроль определяются шансы (Odds) заболевания под действием ВПФ. По определению, шансы - это отношение частоты заболевания к частоте отсутствия заболевания. Шансы и вероятности Р содержат одну и ту же информацию, но по-разному выражают ее: Odds = Р/(1-Р). Логика исследований случай-контроль предопределяет необходимость оценки шансов подверженности ВПФ в группе случаев: Odds[cases] = a/c и в группе контролей: Odds[controls] = b/d .

Характеристикой воздействия ВПФ является величина «отношение шансов» (OR) - отношение шансов заболевания в группе случаев к шансам в группе контролей. OR - основной показатель связи заболеваемости с предшествующими событиями. Оценка OR имеет вид

OR = Odds[случаи] / Odds[контроли] = (a*d ) / (b*c) (15)

Величина OR характеризует увеличение риска заболевания, обусловленного воздействием ВПФ.

Следует еще раз подчеркнуть, что оценка OR специфична только для исследований в формате «случай-контроль». Для эпидемиологии ПОЗ характерны когортные исследования. Формально возможная по результатам таких исследований оценка отношения шансов фактически бессодержательна. Тем не менее, такие оценки нередко встречаются в результатах обследования ситуации с ПОЗ на отдельных предприятиях (см.напр.[7]).

2.3. Сравнение статистических и эпидемиологических выводов. Представляет интерес сравнить критерии достоверности связей между переменными, принятыми в статистике и в эпидемиологии. Как отмечалось в разд.2.1, в статистике такой критерий сводится к условию достаточно большой величины φ (см. табл.2). В эпидемиологии ей можно сопоставить величину этиологической доли EF.

В самом деле, обе величины растут с ростом корреляции между переменными, обе меняются в интервале от 0 (отсутствие корреляции) до 1 (полная коррелированность).

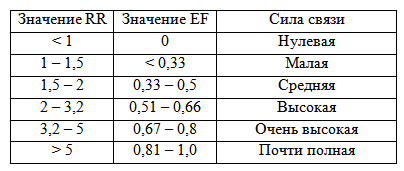
Интерпретация величины EF, принятая в эпидемиологии [8], приведена в табл. 3:

Таблица 3

Интерпретация значений критериев RR и EF

Как видно из сопоставления таблиц 2 и 3, для интерпретации величин критериев φ и EF используются близкие термины, близки также и количественные градации критериев. Тем не менее, следует иметь в виду, что критерии φ и EF определяются различными формулами и могут существенно различаться по величине в одном и том же исследовании. Покажем это.
Предположим, для простоты (это предположение не уменьшает общности вывода), что контрольная группа выбрана равной по численность исследуемой группе, т.е. в табл.1 a+b = c+d = N/2 . В этом случае отношение φ/EF определяется выражением

φ/EF = a/[N*(a+c)]^1/2 (16)

Отношение максимально при с = 0, однако и при этом оно равно (a/N)1/2 << 1. Последнее неравенство следует из того, что обычно количество ПОЗ в коллективе (а) составляет незначительную часть от численности коллектива (N).

Отсюда можно сделать вывод о том, что в эпидемиологии интерпретируются как значительные такие корреляции переменных, которые по общим статистическим критериям были бы признаны незначащими.

3. Эпидемиологическая характеристика респираторной патологии в горно-химической промышленности Крайнего Севера.

3.1. Продемонстрируем возможности использования таблиц сопряженности для анализа бронхолегочной патологии у рабочих, занятых добычей, транспортировкой и обогащением апатит-нефелиновых руд в климатических условиях Крайнего Севера. Исходные статистические данные взяты из работы [9], целью которой было изучение структуры хронических бронхолегочных заболеваний у различных групп рабочих предприятия ООО «Апатит» (Мурманская обл.). При проведении углубленного медосмотра были обследованы 2238 работников подземных рудников (основная группа). В качестве группы контроля были обследованы 790 работников железнодорожного цеха (ЖДЦ). Хронические бронхолегочные заболевания (ХБЛЗ) дифференцировались по нозологическим формам, однако, в связи с иллюстративностью последующего, ниже этого делаться не будет. Авторы [9] выделяли «группу риска», в которую включались лица с некоторыми признаками респираторной патологии, недостаточными для установления диагноза какого-либо ХБЛЗ. Ниже эта группа будет объединена с группой «здоровые лица», т.е. «сомнительные» случаи будут причислены к здоровым.

В рамках принятых предположений таблица сопряженности имеет вид:

Таблица 4

Таблица сопряженности
состояния респираторного здоровья работников

Анализ данных табл.4 с использованием соотношений п. 2.1 и п.2.2 позволяет утверждать следующее:

• Оценочный риск ХБЛЗ в обследованном коллективе составляет Р(ПОЗ=1) = 0,146.
• Риск возникновения ХБЛЗ в группе, подвергающейся воздействию ВПФ, составляет Р(ПОЗ=1|ВПФ=1) = 0,173.
• Риск возникновения ХБЛЗ в группе, не подвергающейся воздействию ВПФ, составляет Р(ПОЗ=1|ВПФ=0) = 0,07.
• Относительный риск RR = 2,48 ; соответственно, этиологическая доля EF = 60% . Согласно Руководству [8] такие величины RR и EF свидетельствуют о высокой степени причинно-следственной связи нарушений здоровья с работой (см. также табл.3).
• Атрибутивный риск AR = δP = 0,103 . Эту величину можно интерпретировать так, что более 10% заболеваний работников обусловлены действием ВПФ.

3.2. Представляет интерес сравнить сделанный выше вывод о высокой степени причинно-следственной связи обусловленности нарушений здоровья условиями труда с результатом чисто статистического анализа содержимого табл.4.

• Подставляя величины а,b,с и d в формулы (10) и (11) для критерия φ, получим φ ≈ 0,13 . Согласно табл.2, такая величина критерия свидетельствует о слабой связи ПОЗ с действием ВПФ. Этот вывод не совпадает с тем, который следует из полученной выше оценки EF: степень причинно-следственной связи нарушений здоровья с работой следует признать высокой.

Выявившиеся различия между результатами эпидемиологического и статистического анализа результатов по уровням ПОЗ свидетельствуют о большей чувствительности эпидемиологического критерия. Можно полагать, что это обстоятельство обусловлено высокой значимостью эпидемиологических выводов: статистический анализ более «нейтрален», а заключения по его результатам не столь ответственны.

4. Обобщение на случай нескольких заболеваний.

4.1. Как отмечалось выше (см.разд.1), в эпидемиологии ПОЗ существует специфическая проблема множественности НФ реакции организма работников на воздействие ВПФ. Один и тот же фактор может вызывать различные заболевания. В этом случае таблица сопряженности становится многомерной. Для ее анализа можно использовать те же методы (см.напр.[4]), что и для одномерных таблиц, однако, результаты не допускают непосредственной интерпретации в эпидемиологических терминах.

Обычно для общей характеристики ситуации с условиями труда на производстве используется результат суммирования данных по заболеваниям различных НФ [10]. Такую характеристику нельзя признать удовлетворительной по ряду причин.

Во-первых, результат зависит от выбора учитываемых НФ заболеваний. Чем больше НФ принимается во внимание, тем выше получается общий уровень ПОЗ на обследуемом предприятии. Это привносит субъективный фактор в результаты обследования.

Во-вторых, ПОЗ относительно редких НФ (заболевания кожи, остеоартрозы суставов, невропатии) дают небольшой вклад в суммарную заболеваемость, однако их информативность в качестве признаков неблагополучия с условиями труда может быть весьма высока.

Последнее можно скомпенсировать, если в качестве характеристики заболеваемости использовать не абсолютные, а относительные уровни. Например, суммировать не количество заболеваний, а относительные риски: использовать соотношения разд.2 для оценки относительных рисков раздельно для каждой формы заболеваний, общая оценка при этом будет определяться суммой отдельных относительных рисков. Для того, чтобы сделать оценку независимой от количества НФ учитываемых ПОЗ, можно разделить сумму на количество слагаемых. Результирующий относительный риск в этом случае будет определяться формулой

RR = (RR₁ + RR₂ + …) / I (17)

где RR_i - парциальный относительный риск заболевания i-той НФ (i = 1, 2, … , I).

Так определенную величину RR можно использовать так же, как и относительный риск одного заболевания. Например, в соответствии с Табл. 3 - для оценки степени влияния ВПФ на уровень ПОЗ на производстве. Заметим, что правила соответствия, приведенные в этой таблице, можно интерпретировать и как оценку уровней ВПФ по эпидемиологическим данным об уровнях ПОЗ. Особенностью такого подхода является то, что уровни ВПФ оцениваются не в привычных физических (концентрации, потоки, дозы и пр.) единицах, а по той опасности для здоровья работников, которую представляют эти факторы. Так например, если по эпидемиологическим данным относительный риск заболевания не больше 1, потенциальная опасность ВПФ нулевая. При 1 < RR < 1,5 ВПФ представляет малую опасность, при 1,5 < RR < 2 - среднюю опасность и т.д.

При таком подходе заболеваемость становится признаком, указывающим на тот или иной уровень опасности ВПФ на обследуемом предприятии. Для большей наглядности, в случае заболевания одной НФ можно представить некоторую координатную ось, вдоль которой откладывается количественная характеристика заболевания - относительный риск ПОЗ. Ось разбита на интервалы в соответствии с данными в первой колонке табл.3. В зависимости от того, в какой интервал попадают данные по уровням ПОЗ на предприятии, можно судить о степени опасности производственных условий.

Если использовать данные по ПОЗ двух НФ, то признаком будет точка на четвертьплоскости, с введенными на ней координатными осями: RR1 вдоль оси абсцисс и RR2 вдоль оси ординат. Интервалам разбиения возможных значений результирующего относительного риска соответствуют разбиения четвертьплоскости границами - прямыми линиями с уравнениями

2*RR = RR₁ + RR₂ (18)

в которых величина RR принимает значения, заданные в первой колонке табл.3. Попадание изображающей точки в одну из областей между границами указывает на соответствующую степень опасности производственных условий.
В общем случае ПОЗ нескольких НФ, уравнения (17) с подстановками величин RR из табл.3 определяют гиперплоскости в пространстве признаков с размерностью I. Эти гиперплоскости разделяют слои, соответствующие различным степеням опасности производственных условий.
4.2. Стоит отметить, что реально в выражении (17) суммируются вероятности (парциальные риски R_1i ) возникновения заболевания i-той НФ в группе, подверженной воздействию ВПФ. Суммирование происходит с весом W_i = 1/(I*R_0i ) . Вообще говоря, такие значения весов в выражении (17) для результирующего риска содержат определенный произвол. Формула (17) допускает очевидно целесообразное обобщение

RR = W₁*RR₁ + W₂*RR₂ + … + W_I*RR_I (19)

где вес W_i должен определяться по результатам эпидемиологических исследований ПОЗ. Эта проблема, однако, имеет вполне самостоятельный характер для того, чтобы стать предметом отдельного рассмотрения.

4. Заключение.

Эпидемиология профессиональных заболеваний, имея дело с ВПФ, как этиологическими факторами, находится в выигрышном положении по сравнению с другими разделами медицины. Она наиболее приближена к вредным условиям производства, а также к развитию профессионально обусловленных заболеваний. Профэпидемиология, благодаря системе обязательных периодических медосмотров, оказывается ближе других разделов медицины к начальным проявлениям заболеваний, что открывает возможности разработки мер их своевременной профилактики и лечения. Однако, для того, чтобы использовать эти преимущества, общероссийская информационная система АС "Профессиональные риски" должна получать информацию определенной структуры. В качестве шаблона такой структуры могут использоваться таблицы сопряженности признаков «ВПФ-ПОЗ»

Развитые в настоящее время методы анализа и интерпретации содержания таблиц сопряженности (либо в простейшем варианте 2х2, либо в более сложных многоуровневом и многомерном вариантах) создают научную основу для градации условий труда по результатам анализа эффектов реально многофакторного воздействия ВПФ.

Проблема множественности откликов организма работников на воздействие ВПФ является специфической для эпидемиологии профессиональных заболеваний. Для анализа многомерных в этом случае таблиц сопряженности необходимы новые интерпретации результатов в эпидемиологических терминах. В частности, требуются исследования сравнительной информативности заболеваний различных НФ в качестве признаков неблагополучия с условиями труда на обследуемом производстве.

Литература.

1. Федорович Г. В. Структура данных для статистического анализа профессионального риска // Безопасность и охрана труда. - 2012. - № 2.- С.54-55.
2. Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях. - М.: Медицина, 1975 - 295 с.
3. Тимофеева Е.И., Федорович Г.В. Экологический мониторинг параметров микроклимата. - М.: НТМ-Защита, 2007 - 212 с.
4. Аптон Г. Анализ таблиц сопряженности (пер. с англ.). - М.: Финансы и статистика, 1982 - 143 с.
5. Федорович Г. В. Классификация условий труда по эпидемиологическим данным // Безопасность и охрана труда. - 2011. - № 4.- С.49-52.
6. Федорович Г. В. Профессиональный риск. Количественная оценка и управление // Безопасность и охрана труда. -2012. - №1. - С.45 - 50.
7. Аскарова З.Ф., Денисов Э.И. Оценка профессионального риска нарушений здоровья работников горнодобывающей промышленности // Бюллетень ВСНЦ CO РАМН. - 2009 - №1. - С.9 - 14.
8. Р 2.2.1766-03 «Руководство по оценке профессионального риска для здоровья работников. Организационно-методические основы, принципы и критерии оценки».
9. Сюрин С.А., Буракова О.А. Респираторная патология в горно-химической промышленности Крайнего Севера // Безопасность и охрана труда. - 2012. - № 4. - С.56-59.
10. Молодкина Н.Н., Радионова Г.И., Денисов Э.И. Обоснование критериев профессионального риска // Профессиональный риск / Измеров Н.Ф. (ред). - М.: Социздат, 2001. - С. 48 - 55.