Классификация условий труда по эпидемиологическим данным

Г.В.Федорович
д.ф.-м.н., технический директор
ООО «НТМ-Защита» Москва

Введение.

Поправки в Трудовой кодекс, содержащиеся в проекте Федерального закона «О внесении изменений в статьи 17 и 22 Федерального закона «Об обязательном социальном страховании от несчастных случаев на производстве и профессиональных заболеваний», предусматривают категоризациию всех предприятий по условиям труда. Исследования, определяющие классы условий труда (КУТ) на предприятии прямыми методами, на основе измерений параметров производственной среды и трудового процесса, требуют значительных затрат времени и средств. Достаточно указать на стоимость аттестации одного рабочего места 3 – 10 тыс. руб., чтобы оценить финансовые затраты на АРМ всех рабочих мест в стране суммой 0,15 – 0,5 трлн. руб. Это достаточно большая сумма, для того, чтобы имело смысл рассмотреть возможность ее уменьшения.

Существует возможность оценивать КУТ на предприятии косвенным методом - по медицинским показателям здоровья работников. Именно, условия труда можно оценивать по статистическим данным о производственно обусловленной заболеваемости с временной утратой трудоспособности (ВУТ). Как показано ниже, обработка таких данных хорошо алгоритмизируется, что позволит получать результаты оперативно и практически (по сравнению с приведенными суммами) без дополнительных финансовых затрат.

В основе предлагаемого метода лежат выполненные в 90-х годах в НИИ Медицины Труда РАМН исследования по статистическому обоснованию критериев и показателей оценки частоты и длительности ВУТ у работающих в зависимости от условий воздействующих факторов производственной среды и трудового процесса [1] и [2]. В целом предложенные критерии могут быть использованы для решения вопросов о мерах защиты работающих. Тем не менее, как отмечают сами авторы, в зависимости от условий труда, тяжести и напряженности трудового процесса, величины критериев колеблются в достаточно широких пределах. В некоторых случаях метод приводит к противоречивым оценкам (ниже приведены примеры такого рода). Причина очевидна: при анализе результатов статистических исследований следует отказаться от детерминированной логики непосредственного сопоставления данных с наперёд заданным шаблоном. Адекватным инструментом здесь является более гибкая, вероятностная логика, использующая для сравнения условные вероятности. Техника такого сопоставления хорошо разработана. Это классификатор на основе Байесовской вероятностной логики (см. напр.[3]), позволяющий непротиворечиво и эффективно интегрировать различные статистические показатели в единый количественный критерий степени вредности и опасности производственных условий. Развитие таких методов позволит выявлять неблагополучные производства и отдельные подразделения на производстве с вредными условиями труда, используя медицинскую статистику заболеваний с ВУТ.

Ниже демонстрируется работа такого классификатора на примере результатов обследования нескольких производственных объектов [4], [5]. В рассматриваемой задаче логика и арифметика Байесовского анализа вполне тривиальны. Это сделано специально для того, чтобы не заслонять идеи классификации математическими сложностями. Алгоритм классификации основан на принципе максимума апостериорной вероятности. Для классифицируемого объекта вычисляются функции правдоподобия для каждого из классов условий труда (КУТ), по ним вычисляются апостериорные вероятности классов. Объект относится к тому классу, для которого апостериорная вероятность максимальна.

Применительно к рассматриваемой проблеме классификации условий труда, будем считать, что для каждого КУТ известна априорная вероятность P(КУТ) того, что изучаемый объект (условия труда работников) относится к этому классу. В качестве функции правдоподобия будем использовать априорно известное распределение параметров ВУТ – количества случаев К и суммарной длительности D (для определенных численности коллектива и длительности периода наблюдения) по каждому из классов Р(К,D|КУТ). Решением задачи классификации является алгоритм

в котором величина P(КУТ)*Р(К,D|КУТ) интерпретируется как апостериорная вероятность того, что диада (K,D) принадлежит выбранному классу КУТ. Перебор возможных классов определяет максимум апостериорной вероятности (1), именно он принимается за наиболее вероятный КУТ [3].

Основная проблема – в определении вероятностных характеристик причинно-следственных связей в системе «условия труда – длительность ВУТ». Эта проблема плохо формализуема, многое здесь необходимо постулировать, именно эти вопросы требуют обсуждения специалистов.

1.Априорные вероятности

В качестве априорных вероятностей P(КУТ) различных условий труда можно использовать статистические данные Роструда. В Приложении 8 к отчету [6] дана сводная таблица количества рабочих мест с различными КУТ по федеральным округам РФ и по стране в целом. Часть ее приведена ниже (первые две строки).

Доля объектов данного класса в выборке обследованных рабочих мест по стране в целом может быть принята в качестве априорных вероятностей. Следует лишь перейти от процентного состава рабочих мест (вторая строка табл.2) к десятичным долям (третья строка).

Априорной оценкой условий труда работников является его оценка по гигиеническим критериям [2]. При анализе профессионально обусловленной заболеваемости с ВУТ использовались оценочные шкалы, рассчитанные на основе статистического анализа показателей профессиональной заболеваемости по стране. Представляющие интерес для дальнейшего результаты исследования [2] зависимости показателей ВУТ от КУТ приведены в первых трех колонках табл.2.

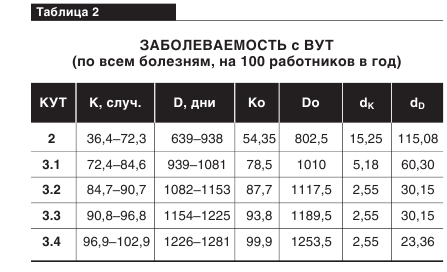
Наглядное изображение областей, соответствующих различным условиям труда на плоскости (K,D) приведено на рис.1.

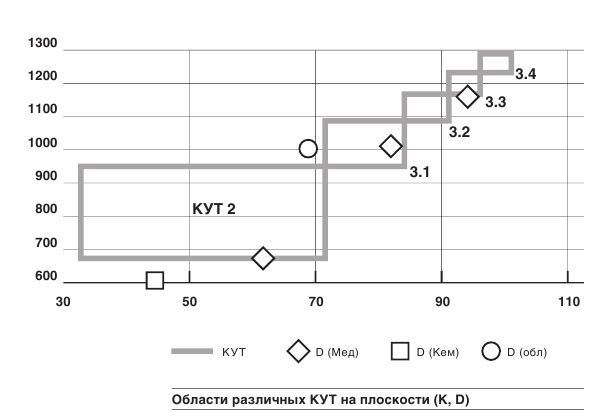
Для каждого конкретного производства значения параметров ВУТ определяют точку на плоскости (K,D). В зависимости от того, в какую из областей попадает определяющая точка, выносится суждение о принадлежности условий труда на обследуемом производстве к тому или иному классу.

Обращает на себя внимание незначительность доли классифицированных областей по сравнению с областями возможных наборов параметров ВУТ. В литературе опубликованы данные по конкретным производствам, для которых значения параметров ВУТ определяют точку на плоскости (K,D), лежащую вне классифицированных областей. Это можно сказать о рабочих различных производств предприятия по производству рафинированной меди ОАО «Уралэлектромедь» [5] (отмечены ромбами на рис.1), о работниках ООО «Химволокно» Кемеровской обл. [4] (отмечено кружком на рис.1), а также о средних показателях ВУТ для рабочих производств в г. Кемерово [4] (треугольник на рис.1). Мыслимы и другие ситуации, когда непосредственное сопоставление параметров ВУТ с данными табл.1 не приводит к сколько-нибудь обоснованным суждениям о КУТ на соответствующем производстве.

Причина невозможности непосредственного использования табл.1 для классификации производства по КУТ состоит в статистическом характере исходных данных. Как уже отмечалось во Введении, при анализе результатов статистических исследований следует отказаться от детерминированной логики непосредственного сопоставления данных с наперед заданным шаблоном. Адекватным инструментом, приводящим к адекватным по существу и по форме заключениям, здесь является более гибкая, Байесовская (вероятностная) логика, использующая для сравнения условные вероятности. Преимуществом является то, что в качестве исходных данных для проведения классификации можно использовать любые наборы (K,D), ответ имеет вероятностный характер – дает вероятность принадлежности условий труда на обследуемом производстве к тому или иному классу. Одновременно определяется возможная ошибка отнесения условий труда к другому КУТ.

Приведенные в табл.2 диапазоны возможных значений числа случаев K и суммарной длительности D заболеваний с ВУТ обусловлены, в основном, тем, что внутри одного класса допускаются значительные изменений условий труда. Кроме того, данные табл.1 не дифференцированы по различным производствам, характеризующимся факторами вредности различной природы.
Проведенный в [7] и [8] анализ возможных подходов к описанию статистических характеристик ВУТ в трудовых коллективах показал целесообразность рассмотрения средних по ансамблю, т.е. по неограниченному числу копий исследуемой системы, находящихся в одинаковых макроскопических состояниях. При этом микроскопические состояния системы могут принимать все возможные значения, совместимые с заданными значениями макроскопических параметров, определяющих её макроскопическое состояние.

Построим совместимую с этим подходом модель обследования коллектива из N работников. Выяснение вопроса о том, болен ли один из работников можно представить как испытание с двумя возможными исходами х: да (х = 1) или нет (х = 0). Обследование коллектива при этом представляется как проведение N независимых испытаний, результатом которых является совокупность N исходов {x₁, x₂, …, x_N}. Это типичное исследование по схеме Бернулли [9]. Вероятность появления n = Σ_i x_i положительных ответов определяется биномиальным распределением

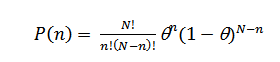
(2)

Среднее значение n при этом определяется как <n> = N*Θ , среднеквадратичное отклонение n от <n> определяется как d = [n*Θ*(1-Θ)]1/2. При больших N (реально необходимо d2 >> Θ), согласно предельной теореме Муавра-Лапласа, можно [9] использовать нормальное распределение Гаусса вместо биномиального распределения.

Пересчет (см.напр. [7]) числа n случаев заболевания с ВУТ в их суммарную длительность D сводится к умножению n на длительность Y периода наблюдения (обычно принимается один год: Y = 365 дней). Если известна средняя продолжительность l болезни, то число случаев К за период наблюдения определяется соотношением К = D/l . Использование этих соотношений позволяет функцию распределения (2) для n трансформировать в функции распределения для D и K .

Реальная ситуация сложнее из-за отмеченного выше вклада в разброс параметров D и K таких факторов, как изменения условий труда в пределах одного класса и различия в природе вредных факторов на различных производствах. Тем не менее, вид функции распределения целесообразно сохранить нормальным, подобрав параметры (центр и ширину) распределений.

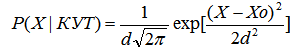
(3)

Параметры функции – центр распределения Хо и среднее квадратическое отклонение d – можно определить с использованием данных первых колонок табл.2 , предполагая, что в них приведены полуширины распределений. В рамках этого предположения получим для каждого КУТ от 2 до 3.4 центры распределений K_o и D_o, а также средние отклонения d_K и d_D . Эти величины приведены в последних четырех колонках табл.2. Соотношение (3) вместе с приведенными в табл.2 данными по центрам и отклонениям параметров K и D достаточны для описания функций правдоподобия для различных КУТ. Это справедливо, если ограничиться моделью наивного Байесовского классификатора, включающего в набор исходных аксиом предположение о независимости признаков, определяемых указанными параметрами. Формализация этого предположения сводится к подстановке в (1) соотношения

Р(К,D|КУТ) = Р(К|КУТ)* Р(D|КУТ)

Здесь величины плотностей вероятностей Р(К|КУТ) и Р(D|КУТ) определяются по формуле (3) после замены Х на К, Х_о на К_о, d на d_K и аналогично для D. Предположение о независимости существенно упрощает задачу, так как определить две одномерные плотности легче, чем одну двумерную.

2. Результаты классификации условий труда.

Продемонстрируем работу описанного алгоритма классификации условий труда на примере заболеваемости с ВУТ рабочих медеплавильного цеха предприятия по производству рафинированной меди ОАО «Уралэлектромедь» [5].
Заболеваемость с ВУТ различных групп рабочих изучалась методом ее углубленного (индивидуального) учета с последующей группировкой болезней в соответствии с [10]. Кроме плавильщиков, из рабочих того же цеха были выделены ремонтные и вспомогательные профессии (прочие). В качестве контроля была использована группа рабочих-мужчин ремонтных и вспомогательных профессий цеха электролиза меди, не подвергающихся воздействию производственных вредностей огневого рафинирования меди. Для этих групп работников были определены характерные параметры заболеваний с ВУТ : количество К случаев в пересчете на 100 человек и суммарная длительность D ВУТ за год наблюдения. Результаты приведены в первых строках табл.3

Колонки 2 – 4 отведены под результаты классификации условий труда на предприятии ОАО «Уралэлектромедь» [5], в колонках 5 – 6 общие данные по г.Кемерово и отдельно – по химическому производству ООО «Химволокно» (Кемеровская обл.) [4].

В строках 4 – 8 приведены рассчитанные по формуле (1) апостериорные вероятности принадлежности условий труда к тому или иному классу КУТ. Для того, чтобы сделать удобочитаемыми эти результаты, даны десятичные логарифмы вероятностей.

Если сопоставить данные по K и D для работников ОАО «Уралэлектромедь» с априорными распределениями, представленными в табл.2, можно отметить, что для плавильщиков диада (K=82,D=1015) попадает в область, характерную для КУТ 3.1 (72<K<84 , 939<D<1081). Именно к такому выводу приводит использование Байесовского классификатора (см. 2-ю колонку табл.3). Вероятность КУТ 3.1 отличается от 1 не более чем на 1 % . Вероятность принадлежности условий труда плавильщиков к КУТ 2 составляет менее 1% . Для КУТ 3.1 вероятность еще меньше (менее 0,1%).

Для рабочих контрольной группы (4-я колонка в табл.3) диада (K=61,D=647) попадает в область, характерную для КУТ 2 (36<K<72 , 639<D<938). Этот же результат дает Байесовский классификатор, причем возможность другого КУТ пренебрежимо мала (порядка 10-8).
Для рабочих вспомогательных профессий (колонка «Прочие») результат неоднозначен: К = 95 соответствует КУТ 3.3, а D = 1148 соответствует КУТ 3.2 . Здесь обоснованное суждение о наиболее вероятном КУТ можно получить только если использовать Байесовский классификатор (1). Анализ данных в последних пяти строчках этой колонки показывает, что вероятнее всего (с вероятностью 93%) условия труда соответствуют КУТ 3.3. Вероятность КУТ 3.2 составляет ≈ 7% .

Таким образом, для плавильщиков и для контрольной группы результат Байесовского анализа (КУТ 3.1) совпадает с результатом непосредственного сопоставления с данными табл.2. Условия работы вспомогательных профессий (колонка «Прочие») не определяются непосредственно по табл.2. Байесовский классификатор определяют КУТ 3.3, хотя вероятность КУТ 3.2 не пренебрежимо мала.

Заключение.

В работе продемонстрирована возможность оценки КУТ на предприятиях по медицинским показателям здоровья работников. В основе метода лежит анализ статистических материалов, накопленных в 90-х годах в НИИ Медицины Труда РАМН в ходе проведения исследований по обоснованию критериев и показателей оценки частоты и длительности ВУТ у работающих в зависимости от условий воздействующих факторов производственной среды и трудового процесса [1] и [2].

Для анализа таких статистических данных использован хорошо обоснованный и доведенный до эффективных алгоритмов аппарат вероятностного анализа на основе Байесовской логики.

Применение метода оценки КУТ для анализа данных о заболеваемости с ВУТ на различных предприятиях демонстрирует его эффективность и разумность полученных с его помощью результатов.

Рассматривался относительно простой случай двух параметров, определяющих ВУТ: число К случаев заболеваний и суммарная длительность D. Реально представляет интерес дифференциация ВУТ по нозологическому и этиологическому принципам. Это позволит перейти к углубленному Байесовскому анализу профессионально обусловленных заболеваний.

Литература.

1.Молодкина Н.Н. Профессиональный риск и защита здоровья работающих. В сборнике «Пенсионная реформа в России: оценка специалистов». Под ред. Баскакова В.Н. и Орлова А.С., - М.: Редакция журнала "Пенсия", 1999. - 170 с.
2.Молодкина Н.Н., Радионова Г.И., Денисов Э.И. Обоснование критериев профессионального риска. В кн. Измеров Н.Ф. (ред) Профессиональный риск. – М.: Социздат, 2001. – С. 48 - 55.
3.Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. — М.: Финансы и статистика, 1989. – 360 с.
4.Штернис Т.А. Профессиональная заболеваемость и заболеваемость с временной утратой трудоспособности работающих в химической промышленности. // Успехи современного естествознания – 2006 - №4 – С. 108 – 109.
5.Адриановский В.И., Липатов Г.Я., Нарицына Ю.Н. Некоторые результаты изучения заболеваемости с временной утратой трудоспособности рабочих, занятых в огневом рафинировании меди.// Фундаментальные исследования. Медицинские науки. №2, 2010. С.14-18.
6.Состояние условий и охраны труда в субъектах Фоссийской Федерации: Научно-аналитические материалы ВНИИ Охраны и Экономики Труда. М., 2010.- 90 с.
7.Федорович Г.В. Статистика ансамблей в расчетах профессиональных рисков // БиОТ – 2010 - № 4 – С. 48 – 52.
8.Федорович Г.В. Статистические ансамбли временной утраты трудоспособности// Человек и труд – 2011- №3- C. 62-65.
9.Гмурман В.Е. Теория вероятностей и математическая статистика – М.: Высш. шк., 1998. – 479 с.
10.Международная классификация болезней: руководство по международной статистической классификации болезней, травм и причин смерти. - Женева: ВОЗ, 1989. - Т.1. - 757 с.