| Ж-л «Безопасность и охрана труда» № 4, 2010 г., С. 48-52 |
|||||||||||||||||||
|
Статистика ансамблей в расчетах профессиональных рисков |
|||||||||||||||||||
|
Г.В.Федорович, ООО «НТМ-Защита» |
|||||||||||||||||||
|
Введение |
|||||||||||||||||||
|
Планируемый переход от определения профессионального риска в зависимости от вида экономической деятельности к оценке его уровня по фактическому состоянию охра-ны труда на предприятии имеет целью повышение эффективности системы социального страхования от несчастных случаев на производстве и профессиональных заболеваний. Объективную оценку условий труда может дать аттестация рабочих мест, включающая гигиеническую классификацию условий труда. Эта процедура является в настоящее вре-мя наиболее адекватным инструментом ранжирования рисков от опасностей, обусловлен-ных вредными производственными факторами. Для того, чтобы результаты оценки про-фессионального риска можно было бы использовать в практике социального страхования, необходимы математические модели расчета одночислового показателя состояния здо-ровья трудового коллектива по уровням факторов и длительностям их воздействия. В современной науке разработаны весьма эффективные методы исследования сис-тем, состоящих из большого числа подобных объектов. Эти методы первоначально были разработаны в статистической физике, но в настоящее время широко используются в тео-рии сложных систем – экономике, эпидемиологии, социологии и т.п. Следует провести границу между различными употреблениями термина «статистика». В науке и практике часто используются статистические методы обработки результатов наблюдений, позво-ляющие получить объективные критерии для проверки справедливости гипотез, нахожде-ния надежных значений измеряемых величин, для оценки ошибок. Другое понимание термина «статистика» используется в статистической физике. Это аксиоматизированная дисциплина, описывающая свойства систем многих объектов. С общей точки зрения это комбинаторная теория меры (см. напр. [1]). Основными объектами изучения являются макроскопические свойства системы в целом, образование нетривиальных структур и явления самоорганизации и коллективного поведения в таких системах. Именно последнее направление исследований будет использоваться ниже для анализа ситуации с временной утратой трудоспособности (ВУТ) в трудовых коллективах. При этом следует иметь в виду, что свойства систем многих объектов описываются в терминах специфических переменных, характерных для средних по ансамблю: статистическим весом, энтропией, температурой и т.п. Эти переменные не очевидны, они не измеряются непосредственно и могут быть только вычислены по результатам наблюдения за системой. Тем не менее, именно эти переменные дают адекватное описание системы. |
|||||||||||||||||||
|
1. Общие характеристики статистических ансамблей. |
|||||||||||||||||||
| 1.1. Различные описания трудового коллектива как системы из многих объектов. | |||||||||||||||||||
|
Для применения методов статистической физики к трудовым коллективам необходимо учитывать различия в определении средних значений в статистической физике и в меди-ко-социальных исследованиях. В последних принято наблюдать определенные коллекти-вы в течение достаточно продолжительного времени, суммируя при этом исследуемые случаи. Результаты затем нормируются на определенный промежуток времени Y (обычно год, т.е. Y=365 дней) и на определенную численность N коллектива (обычно N=100 чело-век). Основные параметры, описывающие ситуацию – количество К случаев временной утраты трудоспособности (ВУТ) в контролируемом коллективе и полное число дней D с ВУТ. Частное от деления l = D/K естественно считать средней длительностью ВУТ. В статистической физике принято иметь дело с ансамблями состояний системы в оп-ределенный момент времени. При этом среднее по времени заменяется на среднее по ан-самблю (эргодическая гипотеза). Для трудовых коллективов исходными параметрами системы являются: среднее количество n работников с ВУТ в момент наблюдения и M - суммарная длительность ВУТ этих работников. Среднее количество дней ВУТ, приходя-щееся на одного работника равно m = M/N . Соответственно, |
|||||||||||||||||||
|
|
(1) |
||||||||||||||||||
|
Для определения связи между этими параметрами полезно ввести в рассмотрение длительность L периода между случаями ВУТ у одного работника. Очевидно, что при наблюдении за коллективом в течение времени Y количество К случаев ВУТ будет K = N*Y/L (предполагается, что Y < L). Это соотношение дает возможность определить L, ис-пользуя данные о К. Соответственно, соотношение между n и D принимает вид: |
|||||||||||||||||||
|
|
(2) |
||||||||||||||||||
| Как видно, и при описании ситуации с ВУТ, принятом в медико-социальных исследованиях, и в рамках статистики ансамблей для описания системы требуется два параметра: К и D в первом случае, n и m во втором. Преимуществом второго описания является то, что для ансамблей величины n и m не независимы. Они могут быть выражены через такие параметры, имеющие существенно статистическую природу, как информационная энтропия S (термин, введенный К.Шенноном) или, связанная с ней, статистическая температура T. | |||||||||||||||||||
|
1.2. Общие принципы описания статистики ансамблей. |
|||||||||||||||||||
| Согласно общим постулатам статистической физики (см. напр. [2]), практический смысл имеют средние по ансамблю, т.е. по неограниченному числу копий данной систе-мы, находящихся в одинаковых макроскопических состояниях. При этом микроскопиче-ские состояния системы могут принимать все возможные значения, совместимые с задан-ными значениями макроскопических параметров, определяющих макроскопическое со-стояние системы. Система может находиться в любом из I состояний, вероятность которых обозначим через Pr(i), где i = 0, 1,…, I . На вероятности накладывается обычное условие нормировки |
|||||||||||||||||||
|
|
(3) |
||||||||||||||||||
| Средняя по состояниям вероятность <P> определяется по формуле | |||||||||||||||||||
|
|
(4) |
||||||||||||||||||
| Очевидно, что система будет находиться преимущественно в том состоянии, в кото-ром средняя вероятность максимальна. Это обстоятельство можно непосредственно ис-пользовать для определения наиболее вероятного распределения состояний системы, од-нако, полезно предварительно отметить, что вместо взвешенного суммирования вероятностей Pr(i), в (4) можно использовать любую, монотонно растущую функцию от Pr(i). Существуют веские основания (см.напр.[2]) для использования в статистической теории ансамблей информационной энтропии S , определяемой формулой | |||||||||||||||||||
|
|
(5) |
||||||||||||||||||
| Наиболее вероятное состояние системы можно определить как состояние с максимальной информационной энтропией. Если о системе ничего больше не известно, то условие максимума S при выполнении нормировки (3) можно, используя метод неопределенных множителей Лагранжа, записать в виде требования максимума суммы | |||||||||||||||||||
|
|
(6) |
||||||||||||||||||
| Дифференцируя (6) по всем Pr(i), получим набор уравнений | |||||||||||||||||||
|
|
(7) |
||||||||||||||||||
| из которых следует, что все Pi одинаковы и (с учетом условия нормировки (3)) равны 1/N. Если система характеризуется некой экстенсивной величиной Хi, так что i-тому со-стоянию можно поставить в соответствие значение Xi, то среднее значение <Х> по воз-можным состояниям системы определяется формулой |
|||||||||||||||||||
|
|
(8) |
||||||||||||||||||
| Если величину <X> можно считать заданой, то наиболее вероятное состояние опре-делится из условия максимума суммы, аналогичной (6), в которую входит еще один неоп-ределенный множитель Лагранжа | |||||||||||||||||||
|
|
(9) |
||||||||||||||||||
| Дифференцируя каждый член суммы по Pr(i), получим уравнения для Pr(i) | |||||||||||||||||||
|
|
(10) |
||||||||||||||||||
| Отсюда следует | |||||||||||||||||||
|
|
(11) |
||||||||||||||||||
| Нормирующий множитель Z(x) представляет собой статистическую сумму | |||||||||||||||||||
|
|
(12) |
||||||||||||||||||
| Eе можно использовать для определения средней величины <X> вместо формулы (6): | |||||||||||||||||||
|
|
(13) |
||||||||||||||||||
|
1.3. Статистика ВУТ. |
|||||||||||||||||||
| Применим приведенные выше общие результаты статистики ансамблей к трудовым коллективам численностью N человек, некоторые из которых находятся в состоянии про-фессионально обусловленной ВУТ. Длительность ВУТ у каждого из них может составлять i дней (i = 0, 1, …). Суммарная длительность ВУТ у этих работников составляет М дней, т.е. | |||||||||||||||||||
|
|
(14) |
||||||||||||||||||
| Полное число возможных состояний системы с заданной величиной M называется статистическим весом W(M). В рассматриваемом случае это число комбинаций распреде-ления числа M по N членам трудового коллектива: | |||||||||||||||||||
|
|
(15) |
||||||||||||||||||
| C точностью до множителя информационная энтропия S равна | |||||||||||||||||||
|
|
(16) |
||||||||||||||||||
| а статистическая температура T определяется из соотношения | |||||||||||||||||||
|
|
(17) |
||||||||||||||||||
| При выводе последнего соотношения предполагалось, что M >> 1 , N >> 1 и исполь-зовалась формула Стирлинга. Если рассматривать соотношение (17) как уравнение для определения М через температуру Т, то его следует записать в виде | |||||||||||||||||||
|
|
(18) |
||||||||||||||||||
| Можно получить более подробное описание системы из N членов трудового коллек-тива, некоторые из которых находятся в состоянии профессионально обусловленной ВУТ с суммарной длительностью М дней. Например, можно найти вероятность того, что ВУТ одного из членов коллектива будет продолжаться i дней. В этом случае подсистема из оставшихся N-1 человек будет характеризоваться суммарной длительностью ВУТ равной M – i . Следовательно, статистический вес этого состояния равен | |||||||||||||||||||
|
|
(19) |
||||||||||||||||||
| Величина W(M) в данном случае играет роль нормирующего множителя для вероят-ности обнаружения одного из членов коллектива в состоянии ВУТ длительностью i дней: | |||||||||||||||||||
|
|
(20) |
||||||||||||||||||
| Подставляя в (20) формулу (18), определяющую m через Т, получим окончательно | |||||||||||||||||||
|
|
(21) |
||||||||||||||||||
| Первый сомножитель в этой формуле обеспечивает нормировку, второй описывает распределение вероятности ВУТ длительностью i дней. Сравнение выражения (21) с формулой (11) определяет смысл множителя Лагранжа b и статистической суммы Z(b). | |||||||||||||||||||
|
1.4. Здоровье и ВУТ. |
|||||||||||||||||||
|
Для того, чтобы применять результаты п.1.3 к случаям ВУТ в коллективах работни-ков промышленных производств, следует определить границу между здоровыми и забо-левшими работниками. Обычно считается, что работа при соблюдении гигиенических нормативов в течение всего рабочего стажа не должна вызывать заболеваний или откло-нений в состоянии здоровья, обнаруживаемых современными методами исследований, в процессе работы или в отдаленные сроки жизни настоящего и последующего поколений [3]. Можно предположить, что здоровый работник – это тот, кто не болеет ни одного дня. Вероятность обнаружить такого согласно (21) равна Pr(0) = [1-exp(-1/T)] . В практике гигиенического нормирования принято к допустимым условиям труда относить и такие, при которых возможные изменения функционального состояния орга-низма восстанавливаются во время регламентированного отдыха или к началу следующей смены и не оказывают неблагоприятного действия в ближайшем и отдаленном будущем на состояние здоровья работника и его потомство. Вероятность обнаружить такого работника, согласно (21) равна Pr(0) + Pr(1) = [1-exp(-1/T)]2 . Следует иметь в виду, что реально количество дней, пропущенных по ВУТ, обычно определяется по больничным листам, за которыми обращаются, как правило, не в первый день недомогания, а на следующий день после появления первых признаков болезни. Поэтому границу между так определяемыми «больными» и «здоровыми» можно задать количеством дней болезни i*, после которых обращаются за больничным и с которого начинается отсчет ВУТ. Значение i* можно считать латентным периодом ВУТ. Через величину i* вероятность считаться больным определяется как exp(-i*/T), соответственно, используя обозначения, введенные в п.1.1 для среднего количество n работников с ВУТ, имеем |
|||||||||||||||||||
|
|
(22) |
||||||||||||||||||
|
Величина i* определяется «обычаями» и «настроениями» в трудовом коллективе. Как показывает анализ статистических данных по ВУТ, в трудовых коллективах различ-ных производств величина i* примерно одинакова и равна 1,5 – 2. (1) По определенному за время Y для коллектива из N работников количеству D дней с ВУТ определяется величина n и далее, по формуле (22) – статистическая температура Т для обследуемого производства. (2) По температуре вычисляется среднее количество m дней с ВУТ на одного работ-ника (формула (18)) и полное их число М на весь коллектив М = N*m. (3) Количество К случаев ВУТ для всего коллектива определяется из условия K*M*Y = D2 , являющегося следствием соотношения (2). Таким образом, статистическая температура T определяет как количество К случаев ВУТ, так и их длительность D в коллективе из N работников за промежуток времени Y дней. Соответственно, она может служить одночисловым параметром, определяющим риск ВУТ от неблагоприятных условий труда на обследуемом производстве. |
|||||||||||||||||||
|
2. Примеры статистического описания ситуаций в трудовых коллективах. |
|||||||||||||||||||
|
Проиллюстрируем общие принципы, изложенные в п.1, на примерах обследования реальных производств. 2.1. В работе [4] приведены подробные результаты изучения заболеваемости с ВУТ рабочих (как мужчин, так и женщин) медеплавильного цеха предприятия по производству рафинированной меди ОАО «Уралэлектромедь». Они сведены в табл.1. |
|||||||||||||||||||
|
Таблица 1. |
|||||||||||||||||||
|
Уровни заболеваемости с ВУТ рабочих-мужчин основных и прочих профессий |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Заболеваемость с ВУТ различных групп рабочих изучалась методом ее углубленного (индивидуального) учета с последующей группировкой болезней в соответствии с [5]. Кроме плавильщиков, из рабочих того же цеха были выделены ремонтные и вспомога-тельные профессии (прочие). В качестве контроля была использована группа рабочих-мужчин ремонтных и вспомогательных профессий цеха электролиза меди, не подвергаю-щихся воздействию производственных вредностей огневого рафинирования меди. Результаты расчетов статистических характеристик для коллективов различных групп рабочих приведены в таблицах 2-4. Так, в таблице 2 приводятся результаты для плавильщиков (группа 1). Колонка «L» содержит данные о периодичности заболевания, «n» - среднем количестве одновременно болеющих, «l» - средней длительности болез-ней. Видно, что по количеству болеющих на первом месте стоят костно-мышечные расстройства, а по продолжительности – инфекционные болезни. Судя по статистической температуре, характеризующей различные заболевания, профессиональный риск наиболее велик для костно-мышечных расстройств и травм. В последней колонке таблицы 2 приведены данные по срокам начала ВУТ (практически – по срокам обращения за больничным). Дольше всего латентный период длится для костно-мышечных и инфекционных заболеваний и травм – более 2-х дней. Быстрее всего обращаются за больничным с мочеполовыми и кожными болезнями. |
|||||||||||||||||||
|
Таблица 2. |
|||||||||||||||||||
|
Статистические характеристики ВУТ рабочих-мужчин, занятых |
|||||||||||||||||||
|
|
|||||||||||||||||||
| Аналогичные данные по рабочим других специальностей, занятых в цехе огневого рафинирования меди, приведены в таблице 3. | |||||||||||||||||||
|
Таблица 3. |
|||||||||||||||||||
|
Статистические характеристики ВУТ рабочих-мужчин в цехе |
|||||||||||||||||||
|
|
|||||||||||||||||||
| В этой группе по количеству болеющих на первом месте стоят травмы, а по длитель-ности – болезни кровообращения. Они же определяют наиболее серьезный профессио-нальный риск (судя по статистической температуре). Травмы для этой группы рабочих стоят на втором месте. Для травм и болезней кровообращения наиболее велик латентный период ВУТ - он длится более 2-х дней. В таблице 4 приведены данные для рабочих контрольной группы (ремонтные и вспо-могательные профессии). |
|||||||||||||||||||
|
Таблица 4. |
|||||||||||||||||||
|
Статистические характеристики ВУТ рабочих-мужчин контрольной группы. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Сопоставление с результатами для рабочих 2-й группы показывает, что за исключени-ем существенно меньшего риска заболеваний органов кровообращения, данные по кон-трольной группе близки к данным по 2-й группе. Болезни костно-мышечных органов оп-ределяют наибольшие отличия между плавильщиками и контрольной группой: статисти-ческая температура для первой группы 0,4 дня, для третьей 0,3 дня. В последнем случае профессиональный риск меньше. По поводу данных, приведенных в табл.2-4 следует сделать одно замечание, важное для понимания специфики расчетов средних по ансамблю. В последних строках этих таб-лиц, обозначенных «Всего», приведены расчеты, основанные на суммарных данных по классам болезней из табл.1. Видно, что рассчитанная по этим данным статистическая тем-пература существенно превышает таковую, определенную по отдельным классам заболе-ваний. Отсюда можно сделать вывод, что результаты получаются тем точнее, чем более детализированы исходные данные. Заметим также, что средние статистические темпера-туры существенно отличаются от температур в последних строках табл.2-4. Так, для рабо-тающих в цехе огневого рафинирования меди средняя (по классам болезней) статистиче-ская температура составляет величину 0,31-0,33 дня, в то время как для контрольной группы 3 она заметно меньше: 0, 26 дня. 2.2. Не столь подробные, однако вполне пригодные для обработки данные приведе-ны в работе [6]. Исследования проводились на предприятии химической отрасли респуб-лики Беларусь ОАО «Гродно Азот». В ходе технологического процесса рабочие контактируют с веществами 2 и 3 класса опасности (бензол, циклогексан, циклогексанон, циклогексанол, капролактам, щелочи), Исходные данные, дифференцированные по классам производства (но не по болез-ням), приведены в табл.5. Обозначения – как выше, в табл.2-4. Результат – статистическая температура (и, соответственно, профессиональный риск) существенно выше, чем на за-воде «Уралэлектромедь», однако, это вполне может быть результатом суммирования при-чин ВУТ. Если сравнить результаты с теми, что приведены в строках «Всего» в табл.2-4, результат будет обратным – профессиональный риск на предприятии «Гродно-Азот» меньше, чем на заводе «Уралэлектромедь». |
|||||||||||||||||||
|
Таблица 5 |
|||||||||||||||||||
|
Заболеваемость с ВУТ рабочих за период с 1999-2003 год |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Если ограничиться сравнениями только внутри одного производства «Гродно-Азот», то следует отметить, что риск в подразделениях Аммиак-1 и Лактам-1 существенно мень-ше, чем в других и чем по предприятию в целом. Это же отметил и автор исследования [6], который использовал классификацию работы [7]. 2.3. Если справедливы высказанные выше соображения относительно завышения ве-личины статистической температуры при недифференцированном подходе, то при усред-нении данных по заболеваемости населения отдельных районов должны наблюдаться еще большие значения статистической температуры. Эта гипотеза подтверждается данными по заболеваемости населения с ВУТ в Московской области [8]. Данные, приведенные к принятому выше табличному виду, представлены в таблице 6. |
|||||||||||||||||||
|
Таблица 6. |
|||||||||||||||||||
|
Заболеваемость с ВУТ жителей Московской области |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Заключение. |
|||||||||||||||||||
|
Из изложенного можно сделать ряд выводов. 1. Проведенный анализ статистических характеристик ВУТ в трудовых коллекти-вах демонстрирует эффективность использования средних по ансамблю величин (энтро-пии, температуры) для однопараметрической оценки риска профессиональных заболева-ний. В частности, статистическая температура заметно отличается для различных групп работников, занятых на различных работах на одном и том же предприятии. При сопос-тавлении статистических температур для различных предприятий различия вполне досто-верны и позволяют делать выводы о вредности условий труда на этих предприятиях. 2. Для того чтобы однопараметрическую оценка ВУТ (например, посредством ста-тистической температуры) превратить в оценку риска и связать ее с результатами гигие-нической оценки условий труда, необходимо эти результаты дополнить коррелирован-ными с ними клинико-физиологическими, лабораторными и экспериментальными этиологическими данными. Это позволит формировать интегральные статистические показатели профессиональных рисков, как по отдельным рабочим местам, так и по организации в целом. Такие показатели будут избавлены от недостатков зарубежных систем оценки и управления профессиональными рисками: последние обусловлены высокой степенью зависимости конечного результата оценки от экспертного мнения. 3. Включение процедуры оценки профессионального риска в нормативные право-вые акты, увязывающие с результатами АРМ размер выплат по страхованию от несчаст-ных случаев на производстве и профессиональных заболеваний, может повысить заинте-ресованность работодателей во внедрении эффективной системы снижения профессио-нального риска. Мерой эффективности здесь также могут быть статистические ансамбле-вые характеристики условий труда. |
|||||||||||||||||||
|
Литература. |
|||||||||||||||||||
| 1. Кац М. Вероятность и смежные вопросы в физике. М., Мир, 1965, 406 с. 2. Кубо Р. Статистическая механика. М., Мир, 1967, 268 с. 3. Руководство по гигиенической оценке факторов рабочей среды и трудового процесса. Р 2.2.2006 – 05 М., 2005, 142 с. 4. Адриановский В.И., Липатов Г.Я., Нарицына Ю.Н. Некоторые результаты изучения заболеваемости с временной утратой трудоспособности рабочих, занятых в ог-невом рафинировании меди.// Фундаментальные исследования. Медицинские науки. №2, 2010. С.14-18. 5. Руководство по международной статистической классификации болезней, травм и причин смерти. Т.1 // ВОЗ, Женева, 1989. 757 с. 6. И.П. Щербинская. Заболеваемость с временной утратой трудоспособности рабо-чих ОАО «Гродно Азот» и рабочих, занятых в производстве капролактама и аммиака за период с 1999-2003 год. 7. Ноткин Е.Л. Об углубленном анализе данных заболеваемости с временной не-трудоспособностью. // Гигиена и санитария. № 5, 1979. С. 40 - 46. 8. Семенов В.Ю., Гурова А.Н., Лапшина И.М., Лобанова В.Н. Меры по сниже-нию заболеваемости населения с временной утратой трудоспособности в Московской об-ласти.//Здравоохранение. № 4, 2009. С.10-14. |
|||||||||||||||||||



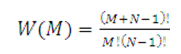
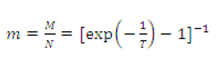
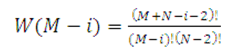
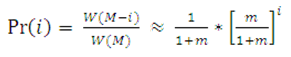
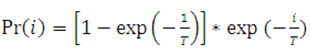
.png)
.png)
.png)
.png)
.png)
.png)


